Warum ist die exakte Speichenlänge so wichtig?

Die Speichenlänge muss exakt bestimmt werden, hier sind nur Toleranzen von rund +-1mm möglich. Ist die Speiche zu lang, dreht der Messingnippel beim festziehen ein neues Gewinde in die Speiche. Dies ist jedoch nicht gleich hoch belastbar, weil die Gewindegänge nicht tief genug sind und dabei Material abgetragen wird. Es handelte sich hier übrigens um eine einfache verzinkte, Stahlspeiche.

Bei der oberen verzinkten Speiche wurde der Nippel zu weit aufgedreht.

Sind die Speichen zu kurz, kann es auch hier zum ausreissen kommen, weil zu wenig Gewindegänge eingeschraubt sind.

Doch wie lang ist die Speiche überhaupt, gemessen wird von Ende des Gewindes - bis - Kopfanfang an der Innenseite, also dort wo der Bogen endet bzw. der Teil der 90Grad zum Speichenmittelteil steht und sich in den Flanschlöchern der Nabe befindet. Bei Straightpull wird ebenso bis Kopfanfang gemessen, nur das es dort keine Aussen- und Innenseite gibt weil der Bogen entfällt.

Speichenlängung

Errechnen der Speichenlänge mittels Formel

Der Speichenrechner errechnet hauptsächlich mittels a) Radius Lochkreisdurchmesser Nabe b) Radius ERD c) Winkel (im Bild 72°) der sich aus Lochzahl eines Nabenflansches und Kreuzung ergibt und nicht etwa wie oft sich die Speichen gegenseitig kreuzen, die Speichenlänge. Wird eine Speiche tangential stärker gewinkelt als eigentlich vorgesehen, steigt die Kreuzungszahl z.B. 2.3x. Umgekehrt sinkt die Kreuzungszahl z.B. 1.7x.

Eine von vielen Formeln der Berechnung der Speichenlänge wäre:

a = Distanz Nabenmittelpunkt bis Flanschmitte links oder rechts
r1 = Radius Nabe, entspricht halben Nabenteilkreisdurchmesser
r2 = Radius der Felge, entspricht halben ERD
m = Anzahl der Speichen pro Flanschseite
k = Kreuzungszahl
alpha = 360° * k / m

2x Kreuzung bei 20Loch

Die blaue Speiche ist im 2. Nabenloch entfernt, wenn man als Ausgangspunkt die rote Linie nimmt. Der Winkel 72° wird in der Formel errechnet durch 360 / x * k. Grün eingezeichnet der Tangentialwinkel der Speiche, dieser wird in der Berechnung nicht verwendet.

Speichenlänge bei Hammerkopfspeichen

Bei Hammerkopfspeichen ist es noch schwieriger, die korrekte Länge zu berechnen. Die herkömmliche Berechnung mit Bogen lässt sich hier nur eingeschränkt übertragen. Der Durchmesser der Speichenlöcher an der Nabe hat hier keine Auswirkung und wird im Berechnungstool auf 0 gesetzt. Der Durchmesser vom Nabenloch hat hier keinen Einfluss darauf wie weit sich die Speiche von der Mitte entfernt. Vielleicht muss man bei manchen Tools den Durchmesser auch auf den Speichendurchmesser setzen. Dies lässt leicht überprüfen indem man die Werte testet und denjenigen verwendet, der die längste Speichenlänge ergibt.

Bei radialer Einspeichung ist es noch einfach zu rechnen aber bei Kreuzung kann man die Werte z.B. 3fach nicht einfach übertragen. Auch ist die Kreuzungsart ja schon durch die Nabe vorgegeben, weil man die Speiche nur noch sehr eingeschränkt winkeln kann. Man kann hier also selbst keine anderen Einspeichmuster wählen, sondern muss sich an die Nabe halten. Am Flansch sitzen 2 Speichenaufnahmen direkt nebeneinander, unmöglich hier eins der üblichen Berechnungstools zu verwenden.

Die Kreuzungsart einer Novatec Nabe mit 12 Speichen auf einer Seite bei der jeweils 2 Speichen auf einer Aufnahme sitzen konnte ich anfangs nur durch Näherung mit Hilfe der linken radialen Seite ausrechnen, bei der aber vorher von einem Systemlaufrad bekannt war, welchen Unterschied die Speichenseite zwischen linker radialer und rechter, gekreuzter Seite betrug. Erst viel später kam ich darauf das man bei der Kreuzungszahl einfach 0,5 addieren muss.

Beispiel: HR Nabe Novatec 24L (12L/12R) Straightpull Carbon FS12SB

LK Durchmesser rechts 48mm
LK Durchmesser links 31,4mm
Abstand Flansch R - Mitte 18.5mm (DT Swiss Spocalc)
Abstand Flansch L - Mitte 35mm (DT SwissSpocalc)
Abstand Flansch L - Aussen (WL) 30mm (rst.mp-all.de)
Abstand Flansch R - Aussen (WR) 46.5mm (rst.mp-all.de)
Einbaumaß 130mm

Bei einer 27.4mm hohen, ungeösten, versetzt gebohrten Remerx Rapid Felge mit ERD 586mm, radialer Speichung d.h. Kreuzung 0 und Speichenlochdurchmesser auf 0 ergibt dies eine Speichenlänge von 278mm.

Da ich nun aufgrund eines fertigen Laufrads von Novatec weiß, daß dort der Längenunterschied zwischen linker und rechter Seite 12mm beträgt, muss ich bei meinem Laufrad rechts 290mm Speichen verwenden. Ich änderte zunächst die Kreuzung solange, bis ich auf diese Speichenlänge kam.

Der DT Swiss Calculator lässt hier leider keine Kommazahlen zu, dies war nur ein Grund um mein eigenes Programm zu schreiben. Auch sind herkömmliche Speichenlängenrechner hier nicht geeignet, dadurch das 2 Speichen direkt nebeneinander sitzen, ganzzahlige Kreuzungsfaktoren also nicht funktionieren.

Bedingt durch die Doppelaufnahmen an der Nabe, wird es etwas komplizierter. Die Nabe hat von der Seite gesehen nur 6 Löcher, aber pro Aufnahme sind 2 Speichen montiert. Bei 6 Doppelaufnahmen muss man sich zunächst einfach weitere 6 in den Zwischenräumen hinzudenken. Man nimmt deswegen 12 Speichen zur Berechnung. Würde man nur 6 verwenden, würden sich ganz andere Tangentialwinkel und Kreuzungszahlen aus der Berechnung ergeben.

Der Speichenrechner arbeitet mit einem Kosinuswert von der Nabe ausgehend, die sich aus Lochzahl pro Seite und Kreuzungszahl ergibt. Man muss sich nur vorstellen, man berechnet im wesentlichen 6 Speichen, auf den echten Flanschen, die alle nur in eine Richtung verlaufen. Die anderen 6 Speichen die auf den 6 virtuellen Flanschen berechnet werden, denken wir uns einfach weg. Das ist aber immer noch nicht ganz korrekt, weil durch die Doppelnahmen (2 Speichen an einer Stelle) stehen die Speichenpaare nun weiter auseinander als bei herkömmlichen Naben mit gleichen Abständen, es ergeben sich dadurch höhere Tangentialwinkel als bei klassischen Naben. Es können daher keine ganzzahligen Kreuzungszahlen verwendet werden.

Bei einer Kreuzung von etwa 2.5 komme ich auf den gewünschten Wert von 290mm. Dies darf aber nur als experimenteller Näherungswert verstanden und nur bei gleicher Anordnung der Speichen angewendet werden.

Dazu kommt noch, daß die Speichen nicht mittig orientiert auf der Doppelaufnahme der Nabe sitzen. Dadurch wird die benötigte Speichenlänge noch einmal 1-4mm je nach Nabe länger oder kürzer. Im Falle der Novatec sind es etwa 1mm. Dies erfordert natürlich das die Speichen nahezu 90 Grad von der Nabe tangential gewinkelt sind. Bei radial wäre dies 0mm. Bestimmen kann man diese Größe mit einem Messschieber, man misst die Breite einer Aufnahme, teilt sie durch 2 und zieht 1mm für den Speichenkopf ab. Oder man montiert 2 Speichen und misst den Abstand von jeweils dort, wo der Kopf anfängt und teilt es durch 2.

USING "STAR" FLANGE SHAPED HUBS To find spoke lengths for "star flange" hubs (including the Zipp 182, 202 and 282 right side flanges), choose a length that is midway between the calculated length for the desired crossing and the calculated length for the next higher crossing. EXAMPLE: For the right side of a 2x rear wheel with the current Zipp 182 model hub: 1. Calculate the 2x and 3x lengths for the right flange 2. Add the 2 figures, then divide the total by 2 to get the correct spoke length for the "star flange"

Das ist die "Näherungsformel" von Zipp. Die Längen kommen in etwa hin, sind aber nicht genau genug.

Nochmal zusammengefasst:

• Lochkreisdurchmesser auf 0 setzen
• Beim Kreuzungsfaktor +0.5 addieren
• Speichenkopf am Flansch ist leicht versetzt bei Kreuzung, diese Strecke (~1-2mm) zur Speichenlänge addieren

Kreuzungsfaktor bei Straightpull errechnen

Auf dieser Seite wird beschrieben, wie man mit Vergleich von Winkeln Kreuzungszahlen mit Dezimalkommastelle errechnen kann. Ich bin mir nicht sicher, ob das wie folgt funktioniert aber es ist ein Ansatz.

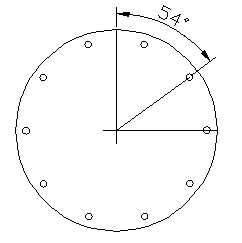
20Loch Standard 2fach Kreuzung. Dies lässt sich errechnen durch:
360 / Lochzahl pro Flanschseite * (Kreuzung - 0.5). Achtung: Diesen Winkel nicht mit tangential Winkel der Speiche verwechseln!

Auf dem obigen Bild sieht man den Winkel bei einer herkömmlichen 20 Loch Nabe mit 2fach Kreuzung. Anders als bei der normalen Speichenlängenberechnung wird hier der Winkel zwischen einem Speichenpaar angegeben. Beim Speichenpaar werden 2 Löcher dazwischen leer gelassen, der linke Teil wird weggelassen, deshalb sind es 54° statt 108°. Bei Straightpull hat man eine etwas andere Darstellung. Zwischen dem Speichenpaar liegt genau mittig eine andere Aufnahme, was bei herkömmlichen Naben nicht der Fall ist. Und darauf kommt es an: Die jeweiligen Speichenpaare haben einen größeren Abstand innerhalb des Paares, dadurch ergibt sich ein höherer Tangentialwinkel und ein höherer Kreuzungswert. Man sieht hier warum Straightpull bei niedrigen Speichenzahlen von Vorteil ist. Allerdings wird der Tangentialwinkel bei 20 Loch Straight Pull 2.5fach mit 99° schon zu hoch als das er einen Vorteil gegenüber Standard 20 Loch 2fach mit 81° hat. Bei 24Loch sieht der Vorteil von Straightpull schon besser aus: Straightpull 2.5fach 84° und Standard 2fach 69°.

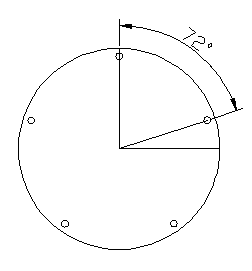
20Loch Straighpull 2.x fach Kreuzung

Die gesuchte Kreuzungszahl ist: 2 + "unser gesuchter Wert", der die Differenz der Winkel darstelt.

Was uns nun zunächst interessiert ist der Winkelunterschied:

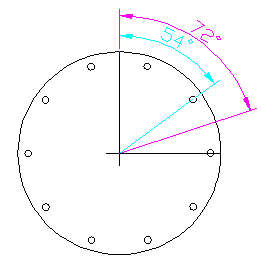
Welcher 72° - 54° = 18° beträgt.

Ein Segment zwischen 2 Speichenlöchern auf einer virtuellen 10Loch Nabenseite hat: 360°/ 10 = 36°.

Um die Kreuzungszahl erhalten, rechnet man 18° / 36° = 0.5. Die normale Kreuzungszahl 2 + 0.5 ergibt 2.5 welche in der Formel zu benutzen gilt, mit einer Lochzahl von 10 pro Seite. Man sieht in dem Bild auch das die gesuchte Differenz genau zwischen 2 Löchern liegt, deswegen 0.5.

Update: Ein Einspeichen einer 28Loch Hinterradnabe mit 7-Sternaufnahme, ergab eine Kreuzung von 3,5. Auch hier sieht man das die 0.5 eine Rolle spielen. Nur wäre man laut den Bildern oben auf 2,5 gekommen. Einen weiteren Hinweis gibt diese Seite von Extralite. Man sieht das die Speichenlänge bei 20L 5-Stern und 28L 7-Stern identisch ist. Somit ist bei 20L 5-Stern ebenfalls 3,5x zu verwenden und bei 24L 6-Stern wie bereits gehabt: 2,5.

Hier ein Hinweis, der für Freunde von Speichen ohne Bogen interessant sein dürfte: Ein einspeichen einer 28Loch Hinterradnabe mit 7-Sternaufnahme, ergab eine Kreuzung von 3,5 bei einem tangentialen Winkel von 95°. Auch hier sieht man das die 0.5 eine Rolle spielen, wie ich schon versuchte rechnerisch (siehe Spokomat: Kreuzungsfaktor bei Straightpull berechnen) zu bestimmen. Nur wäre man laut den Bildern bzw. der Berechnung auf 2,5 gekommen. Einen weiteren Hinweis gibt diese Seite von Extralite. Man sieht das die Speichenlänge bei 20L 5-Stern und 28L 7-Stern identisch ist. Somit ist bei 20L 5-Stern ebenfalls 3,5x zu verwenden und bei 24L 6-Stern wie bereits gehabt: 2,5.

Hinweis: Dies trifft nur auf Naben zu die eine Sternförmige Aufnahme haben und auf jeder Seite eine gleiche Anzahl von Speichen haben.

Bestimmung der Speichenlänge per CAD

Aufgrund der Problematik mit Straightpull in gekreuzter Form und der sehr komplexen Berechnung, habe ich das ganze in einem 2D CAD Programm aufgezeichnet und bin zu vertretbaren Ergebnissen gekommen. Die Sache hat nur den Nachteil, daß es relativ zeitaufwendig ist und man keine Längung darstellen kann. Ich würde daher immer empfehlen, die Längen zu errechnen, auch bei Straightpull.

Grafische Bestimmung in der CAD Freeware Solid Edge

Dabei müssen aber einige Dinge beachtet werden. Durch die laterale Schräge der Speichen, kann dies in 2D nicht dargestellt werden, es muss ein Korrekturfaktor hinzugerechnet werden. Dieser ist an der Zahnkranzseite am kleinsten, da die Speichen dort am steilsten stehen. Ein weiterer Faktor ist die Speichenaufnahme an der Nabe, dieser hält den Anfang der Speiche nicht exakt mittig, es müssen meistens 1-2mm (1mm Novatec, 2mm Mavic) hinzugerechnet werden. Dies berechnet sich aus Flanschbreite / 2 -1mm Speichenkopf.

Im CAD Programm gelingt es nicht immer 100% genau die Maße auf den zehntel mm darzustellen, man sollte den Mittelwert aller Speichen berechnen.

Benutzung von Solid Edge: Ein großer Kreis stellt den ERD dar und ein kleiner den Nabenteilkreisdurchmesser. Diese müssen mit einer Funktion exakt konzentrisch ausgerichtet werden. Die Markierungen für die Speichenlöcher erhält man durch eine benutzerdefinierte Linienart. Der jeweilige Abstand zwischen den Löchern ist auszurechnen und als Linie festzuhalten. Für das jeweilige "Loch" habe ich eine Linienlänge von 0.35mm gewählt. Hier muss auch in der Linienart die Funktion "Zentrieren" statt "Wiederholen" gewählt sein und alle Abstände einzeln eingetragen werden, da sonst die Abstände nicht stimmen und sich in den Zoomstufen ändern. "Fixiert" nicht aktivieren. Etwas komfortabler wäre eine Segmentierungsfunktion der Kreise, die ich aber nicht gefunden habe, mit der Musterfunktion kam ich auch nicht zurecht. Schließlich muss man nur noch die Speichen als Linien einzeichnen.

Hier gibt es eine Beispieldatei für Solid Edge.

Um die Speichenabstände für Solid Edge zu berechnen und um den Korrekturfaktor für die laterale Winkelung zu bestimmen, habe ich ein kleines OpenOffice Calc Sheet erstellt. Ebenso kann man den Kreuzungsfaktor durch vergleichen von Berechnung und Grafik in Erfahrung bringen. Die Formel für die Berechnung der Speichenlänge stammt von Damon Rinard. Ebenso können die lateralen Winkel ausgerechnet werden und der Unterschied zwischen linker und rechter Flanschseite berechnet werden.

Speichenlängen von Systemlaufrädern

Mavic

Bj. 2002

Ksyrium Elite: Rim 23mm, VL/VR 18L radial 283mm M40654 110-130kg, HL/HR 20L 2xcross 303mm M40656 140-160kg ABS nipples
Ksyrium SL SSC: Rim 25mm, VL/VR 18L radial 281mm M40677 100-120kg, HL 10L 3xcross 301mm M40679, HR 10L radial 272mm M40678 130-150kg, OS Zicral spokes

Bj. 2003

Cosmos: Rim ?, VL/VR 20L 20L radial 287mm M40520 80-90kg, HL 10L 3xcross 310mm M40524, HR 10L 3xcross 308mm M40523, 2.3-2.0 round steel spokes ABS nipples

Bj. 2004

Cosmos: Rim 19mm, VL/VR 24L radial 290mm 70-100kg, HL 14L 3xcross 311mm, HR 14L 3xcross 309mm 130-160kg, 2,3-2,0mm round DD steel spokes
Ksyrium Equipe 04: Rim 24mm, VL/VR 20L radial 284mm 70-100kg, HL/HR 24L 2xcross 300mm 130-160kg, 2,3-2,0mm round DD steel spokes
Ksyrium SSC SL 04: Rim 25mm, VL/VR 18L radial 281mm M40677 100-130kg, HL 10L 3xcross 301mm M40679, HR 10L radial 272mm M40678 130-160kg, OS zicral spokes

Bj. 2005

Cosmic Elite: Rim 30,5mm, VL/VR 20L HL 10L radial 285mm 32394601 100-140kg, HR 10L 2xcross 303mm 32394701 135-165kg, Black ultra bladed steel spokes with ABS nipples
Cosmic Carbone SL: Rim 52(19mm*), VL/VR 16L radial 291mm 32390301 105-145kg, HL 10L radial 289mm 32390501 HR 10L 2xcross 307mm 32390401 120-160kg, Black ultra bladed steel spokes with ABS nipples front 2.3 rear 2.6mm thread
Ksyrium Elite 05: Rim 25mm, VL/VR radial 287mm 32389801 115-135kg, HL/HR 2xcross 307mm 32389901 140-165kg, Silver ultra bladed steel spokes with M7 nipples

Bj. 2006

Aksium: Rim 21mm, VL/VR 20L radial 278mm 32419201/32419001 75-90kg, HL/HR 24L 2xcross 302mm 32419301/32419101 130-160kg, Black&Silver profiled steel spokes ABS nipples (fron no straight pull)
Equipe: Rim 24mm, VL/VR 20L radial 284mm 32418601/32418801 75-100kg, HL/HR 24L 2xcross 300mm 32418701/32418901 130-160kg, Black&Silver profiled steel spokes ABS nipples
Ksyrium Elite 700: Rim 25mm, VL/VR 18L radial 287mm 32418401/32389801 115-130kg, HL/HR 20L 2xcross 307mm 32418501/32389901 140-165kg, Black&Silver ultra bladed steel spokes M7 nipples
Ksyrium SL: Rim 25mm, VL/VR 18L radial 281,5mm 32418101 100-130kg, HL 10L cross 301,5mm 32418301, HR 10L radial 272,2mm 32418201 130-160kg, Silver profiled Zicral spokes M7 nipples
Ksyrium ES 06: Rim 22+25mm, VL/VR 18L radial 284,5mm 32417801 100-130kg, HL 10L cross 298,5mm 32418001, HR 10L radial 275mm 32417901 130-160kg, Black profiled Zicral spokes M7 nipples
Cosmic Carbone Pro 06: Rim 51,8mm, VL/VR 16L radial 32390001 271mm 110-140kg, HL 10L radial 270mm 32390101, HR 10L 2xcross 289mm 32390101 140-165kg, Black ultra bladed steel spokes with reversed nipples

Bj. 2007

Ksyrium Elite: Rim 22+25mm, VL/VR 18L radial 290mm 99522301/99522901 100-130kg, HL 10L cross 302mm 99522501/99523101, HR 10L radial 277mm 99522401/99523001 120-145kg, Black&Silver Bladed steel spokes M7 nipples
Cosmic Carbone SL Premium: Rim 52(19mm*), VL/VR 16L radial 291mm 32390301 105-145kg, HL 10L radial 289mm 32390501 HR 10L 2xcross 307mm 32390401 120-160kg, Black bladed steel spokes ABS nipples front 2.3 rear 2.6mm thread

Bj. 2008

Aksium: Rim 21mm, VL/VR 20L HL 10L radial 282,5mm 99607501/99607701 80-90kg, HR 10L 2xcross 305mm 99607601/99607801 150-165kg, Black/Silver bladed steel spokes ABS nipples
Ksyrium Equipe: Rim 24mm, VL/VR 18L radial 278mm 99605701/99606001 80-90kg, HL 10L cross 298,5mm 99605901/99606201, HR 10L radial 274mm 99605801/99606101 130-145kg, Black/Silver bladed steel spokes ABS nipples
Ksyrium SL (Prem): Rim 22+25mm, VL/VR 18L radial 284,5mm 32417801 110-130kg, HL 10L cross 298,5mm 32418001, HR 10L radial 275mm 32417901 120-140kg, Black zicral bladed spokes M7 nipples
Ksyrium SL tub: Rim 22mm, VL/VR 18L radial 284,5mm 32417801 110-130kg, HL 10L cross 301,5mm 99615301, HR 10L radial 278mm 99615201 120-140kg, Black zicral bladed spokes M7 nipples

Bj. 2009

Cosmic Carbone SL: Rim 52(19mm*), VL/VR 16L radial 289mm 99684101 120-140kg, HL 10L radial 288mm 99684301, HR 10L 2xcross 306mm 99684201 140-160kg, Black steel spokes ABS nipples
Ksyrium Elite: Rim 22+25mm, VL/VR 18L radial 284mm 99685601/99686401 110-130kg, HL 10L cross 301mm 99685801/99686601, HR 10L radial 276mm 99685701/99686501 125-145kg, Black&Silver steel spokes M7 nipples

* In den Cosmic Carbone Laufrädern ist der Carbonteil der Felge nur Verkleidung
** Speichenspannungen sind in Kg angegeben, der höhere Wert ist immer nur die Zahnkranzseite
*** Bestellnummern für Speichen sind angegeben, 1. Black 2. Silver falls 2 angegeben

Die Speichenlängen sind im Techbereich ersichtlich.

Shimano

WH-R7800 VR 280mm HL 300mm HR 274mm
WH-R7801 SL VR 282mm HL 300mm HR 274mm
WH-R500 VR 278mm 800-1200N HR 286mm 500-1000N + 900-1500N
WH-R550/560 VR 286mm 980-1400N HL 300/302mm HR 276mm 600-1100N + 1000-1600N
WH-5600/WH-R561/WH-R580 VR 284mm 980-1400N HL 300mm HR 276mm
WH-RS10/20 VR 16x284mm HR 20x300mm
WH-RS30 VR 16x278 HR 20x294mm

Die Längen sind in den Shimano Techdocs ersichtlich.

Rose

Xtreme Lightwheels 1. Generation: VL/VR: 281mm (gerundet 280mm), HR: 285mm (gerundet 286mm), HL: 288mm (16/20L Formula Naben + KinLin XR300 Felgen)
Xtreme Lightwheels 2. Generation: VL/VR: 294mm, HR 293mm, HL: 294mm

Die Laufräder werden bei Xerowheel.com produziert. Dort sind auch Speichenlängen ersichtlich.